Facebook has published a number of programming puzzles to challenge software developers. Their problems are not trivial at all. This is my attempt on "Snack" level problem It's A Small World. Even this one take me sometimes to solve.

The idea is that there are n points on a 2-dimensional plane. For every point, we have to find the 3 nearest neighbors. The naive solution simply match all possible pairs, resulting in O(n²) complexity. The problem requires us to find a better solution than O(n²).

My idea is to divide the plane into a regular grid like below. For example, to find the neighbor of point A, we can focus on cell 2 in the center top and pretty much ignore the points in cell 9 in the lower right. This works very well if the points are randomly distributed. But if many points are clustered together like cell 9, it will work less well. We can recursively partition it into smaller region. But the basic plan should be suffice for this puzzle. The subdivision is a very simple O(n) process.

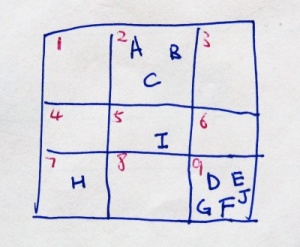
To search for the nearest neighbor, we start from points from the same cell. If this doesn't find the three nearest neighbors we extend into the neighboring cells. The pseudo code is shown below:

  result = None

  for step in 0...n

    cells = find cells "step" away from the source
    min_distance = minimum distance from source to the boundary of the cells

    for all point in cells
        insert distance(source, point) into result

    result = 3 closest points in result

    if there exists 3 points in result those distance < min_distance
        return result

  end for

Of course I'm not the first one to consider these algorithm. Wikipedia has some information on the Nearest neighbor search problem. My solution code is available here. (2010-02-21 Facebook's puzzle server is down. So the solution has not been validated.)

I have decided to put the algorithm into good use. I used it to generate a map of all sizable cities in the world and their nearest neighbors. With 20,000 cities a naive algorithm will need 400 million pairing. Using this algorithm only 10 million pairing are need. It is far from optimal, but good enough to handle Facebook's problem. Also I am curious to use it to find the loneliest city in the world, that is, a city those nearest neighbor is the furthest away. Check the map to find out which city is the loneliest city in the world!

2010.02.21 [programming] - comments